社会人入試silvermoonさんインタビューその3
(それでは面接に関して伺っていきます。実際に受験されたICU国際基督教大学社会人入試の面接はどのような様子でしたか?)
面接は小論があまりにも分からないのである意味で開き直っていました。
流れとしては、最初に志望動機などの話を聞かれました。
私は学びたいものに文系が多かったので、
ICU(国際基督教大学)では理数系もとらないといけないがそれについてどう思うかという質問もされました。
面接官の教授はみなさんやさしいがある意味突っ込んでくるところもあるますね。
(その「理数系の学問もとらなくてはいけないが」という質問にはどのようにお答えになりましたか?)
自分には息子が2人いて新入生の方とほとんど変わらない年齢です。
息子たちは理数系なので、ICUで理数を学ぶ機会があれば、彼らと共通して話せるそれは自分にとってプラスになります。
新しいことを学ぶのは苦ではないし、喜んで自然科学系統の学問も取りたいと答えました。
数学以外は。
(数学は苦手でいらっしゃるのですね?)
数学は全然だめですね(笑)
(他にはどんな質問がありましたか?)
雑談も含めていろんな話題が出ました。
「若い生徒が多い中、社会人としてICUに入学してどんな貢献ができるか」
という質問もされました。
(その質問にはどのようにお答えになりましたか?)
大学に入学する18,19歳は、精神的に半分大人、半分子供です。
不安定な時期ですよね。
自分はアドバイスをしたりということはできないが、彼らの言うことを聞いてあげることはできる。
息子たちと年が変わらないので 理解できるところもあるのではないか、
そんな風に答えました。
(なるほど、実際にICUに入学するとなると、他の学生との年齢差はお考えになりましたか?)
実はかなり悩んだところではあります。
ヨーロッパの大学だと本当に年齢の高い方が多いのです。
どう見ても30?50代という方がたくさん勉強している。
アメリカでもいろんな年齢がいる。
しかし日本ではいまだに社会人が少数派ですね。
ある意味遅れていると思います。
でも人生遅咲きの人間もいますし、大学にいけなかった方もたくさんいます。
戦争があっていけなかった方もいます。
もう少し大学に社会人が入りやすい制度や社会環境があればなとは思いました。
(面接官は何人でしたか?)
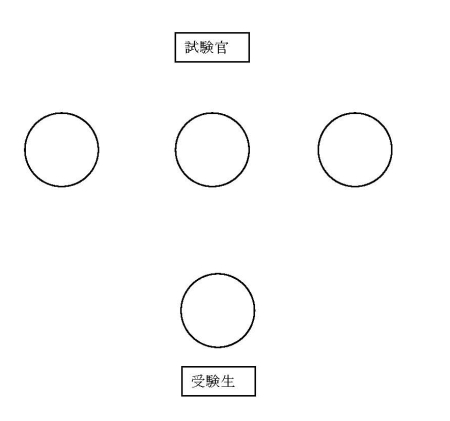
3人の先生がいらっしゃいました。
女性の方が一人ですね。
(3対1ですか。緊張しそうですね)
そうですね、でも入った瞬間にウエルカムなムードでした。
やや記憶が曖昧ですが、先生方は机、受験生は椅子のみだったと思います。
(面接の会場はどちらでしょう?)
建物はICUの本館ですね。
たしか3Fの一教室だったと思います。
小さい机の部屋です。
(次回に続きます)